Posted on by Tina Forsee
A Geometric Construction of the Divided Line by Chris Sonnack
Geometric Divided Line on LogosConCarne
Our starting point is what Plato, in the Republic, says to Glaucon about the divided line. He has introduced the idea of splitting the world into two classes of experience, the visible and the intelligible (also called opinion and knowledge). Plato then says:
Let us represent them as a divided line, partitioned into two unequal segments, one to denote the visual and the other the intelligible order. Then, using the same ratio as before, subdivide each of the segments. Let the relative length of these subdivisions serve as indicators of the relative clarity of perception all along the line.—Republic, Book VI, 509e
Questions arise from that last sentence: Plato’s explanation seems to imply an inequality; that each higher segment, representing greater clarity of thought, should be larger than the one below it. However, it can be demonstrated that the middle two segments must be equal in length.
I first noticed the equality of the middle segments by chance, and after throwing some numbers at the problem and trying some simple fractions, I came up with an algebraic proof. But this didn’t give me much insight into what Plato was thinking. Although the Greeks did have some geometric algebra as well as facilities with numbers, algebra, as we learned it in school, doesn’t show up until about the 9th century, long after Plato.
So I thought I should limit my approach to the geometry of Plato’s time, using only the tools he would’ve used: a straight edge to draw a straight line and a compass to draw a circle of any radius. (For more on this, check out the ‘two tricks’ at LogosConCarne.)
Step 1: We start as simple as possible with a straight vertical line “partitioned into two unequal segments” as shown below.

We label the bottom point a, the top point b. We pick an arbitrary point c to divide the line unequally. (In fact, everything we do here works fine in the degenerate case of equal segments.)
We label the lengths of the bottom segment X and the top segment Y. This gives us a ratio Y:X for the two segments. The total length of the line is X+Y.
Note that a ratio, Y:X, is the same thing as the fraction, Y/X. Here we always put the larger upper length above (or first, in a ratio) and the smaller lower length below (or second) to reflect the idea behind Plato’s vertical line.
Step 2: Draw three straight horizontal lines perpendicular to points a, b, and c, as shown below.
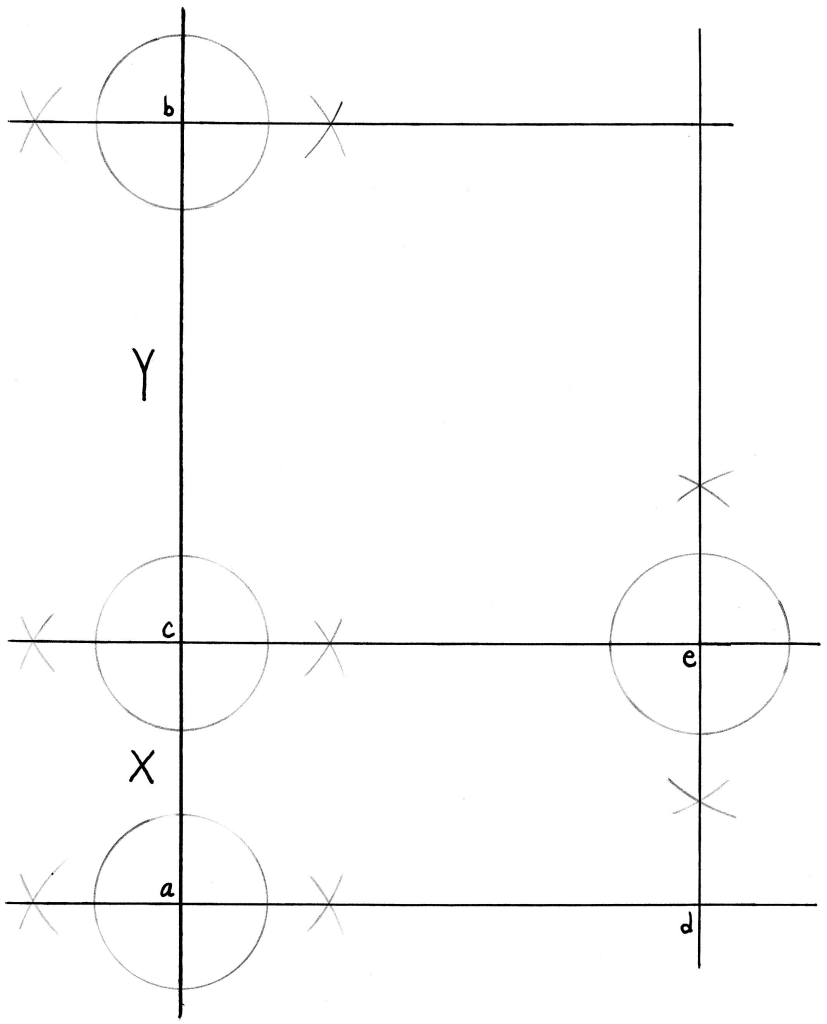
We also pick an arbitrary point d on the lower line and draw a straight vertical line perpendicular to it. The new vertical line intersects the middle horizontal line at point e.
(We care only about the part of those lines to the right, so that’s all I’ve shown. The perpendicular trick obviously results in some extension to the left and, in the case of the new vertical line, below.)
Step 3: Draw a straight (slanted) line connecting point b to point d, as shown below. This line intersects the horizontal line ce at point g. Draw a new vertical straight line perpendicular to line ce such that it intersects point g. The new vertical line intersects the lower horizontal line ad at point f.
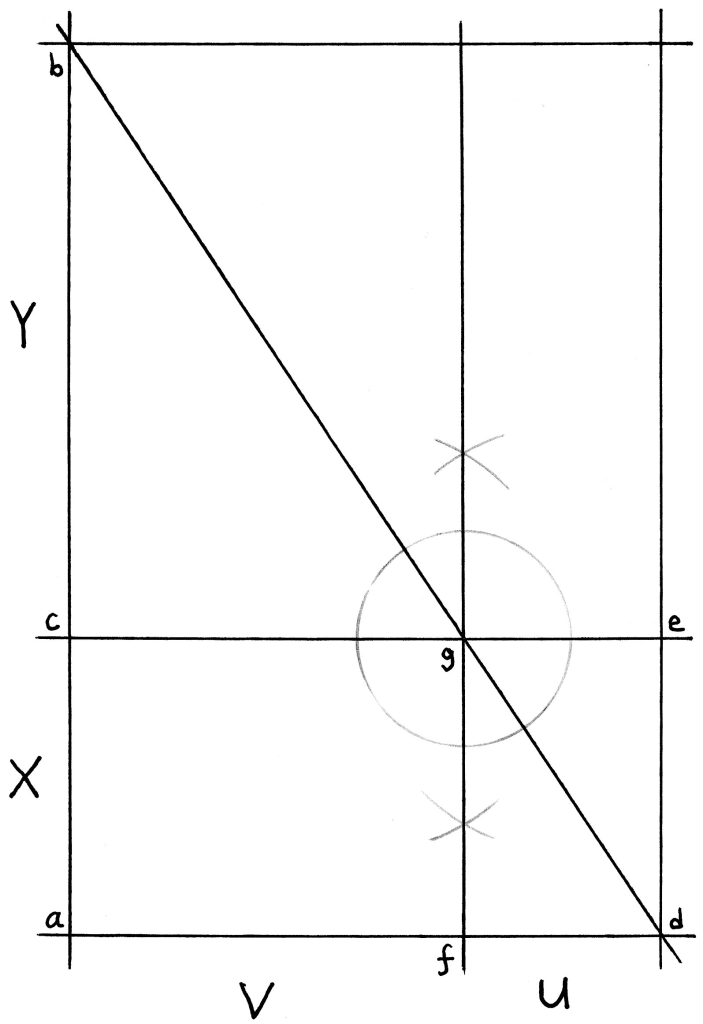
This subdivides the horizontal by the same ratio (but not necessarily the same lengths) as the vertical. This gives us the following equal ratios:
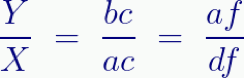
The horizontal ratio matches the vertical one because point g projects down to point f. Think of the slanted line bd as a mirror reflecting the vertical line ab proportionally onto the horizontal line ad. (Because the “mirror” is straight, the reflection can shrink or expand but must remain proportional.)
Step 4: Now we subdivide the vertical line segments and complete Plato’s Divided Line.
Draw a straight slanted line from point b to point e and another from point c to point d (below). The upper one intersects the middle vertical line at point k, the lower one at point h.
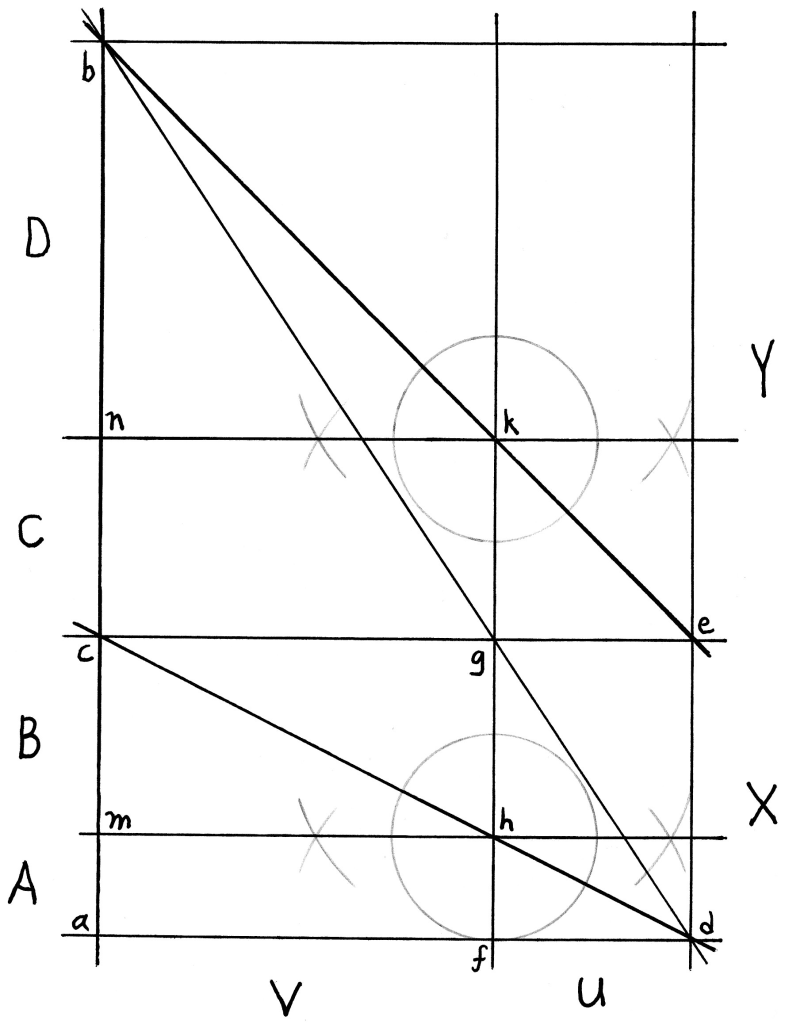
Draw two new straight horizontal lines perpendicular to the vertical lines, one to intersect point k and the other to intersect point h. These intersect the original vertical line (ab) at points m and n.
The new diagonals, line be and line cd, create two new “mirrors” that each reflect the entire horizontal line ad onto, respectively, the upper and lower segments of line ab. Since we know that line ad has the same ratio af:df as the original vertical line (bc:ac), we also know the reflections must be proportional.
Therefore, we have subdivided the segments according to the original ratio as specified by Plato. We label the segments, bottom to top, as A, B, C, and D.
Now all we have to do is prove that B=C.
We start by focusing on the larger upper triangle formed by points c, b, and e, and the smaller lower triangle formed by points a, c, and d. Since they share the same base length (U+V) and have heights according to our ratio Y:X (literally, the height of the upper triangle is Y and of the lower one X), the area of the triangles has the same ratio.
Step 5: Reflect the diagonal line cd by drawing a straight line from point c to a new point r that we create using a compass set to the distance ed (so that ed=er). (As shown below.)
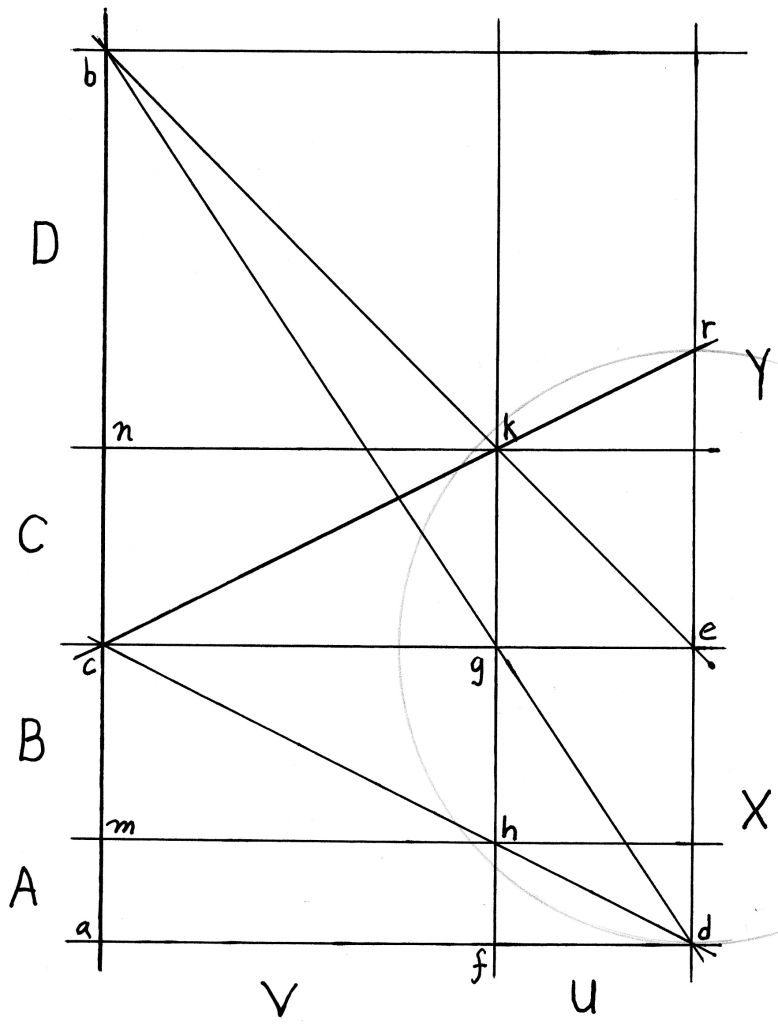
Note that this line intersects point k, and we have a demonstration that B=C, because, if ed=er, then gh=gk, because the triangle crd is an isosceles triangle.
What’s more important is the new triangle formed by cre, which by construction is identical to the original triangle acd. We know the triangles cbe and acd have the Y:X ratio to each other, so the triangles cbe and cre must also have that ratio.
Our advantage now is that their bases overlap and their heights (which have the ratio Y:X) start at the same baseline and extend upwards.
The proof is now in our hands.